
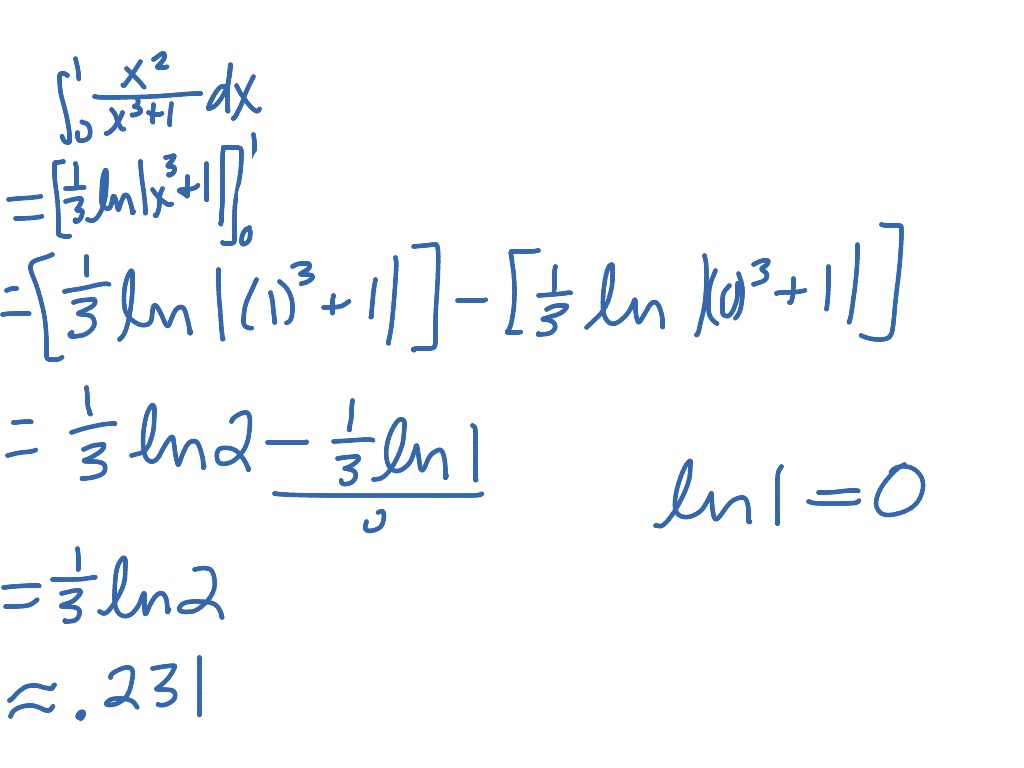
A definite integral of a function is defined as the area of the region bounded by the given function’s graph between two points on a line. By drawing rectangles, we can approximate the actual value of an integral. The area of a region under a curve is represented by an integral. What Do Integrals Mean?Īn antiderivative, Newton-Leibnitz integral, or primitive of a function f(x) on an interval I is denoted by F(x). The function f is referred to as the anti-derivative or integral of f’ in this context. We can determine the function f using the derivative f’ of the function f.

Integrals assign numbers to functions in order to describe displacement and motion problems, area and volume problems, and other problems that arise from combining all of the small data. Integration is the process of obtaining f(x) from f'(x). Integrals are the values of the function discovered through the integration process.
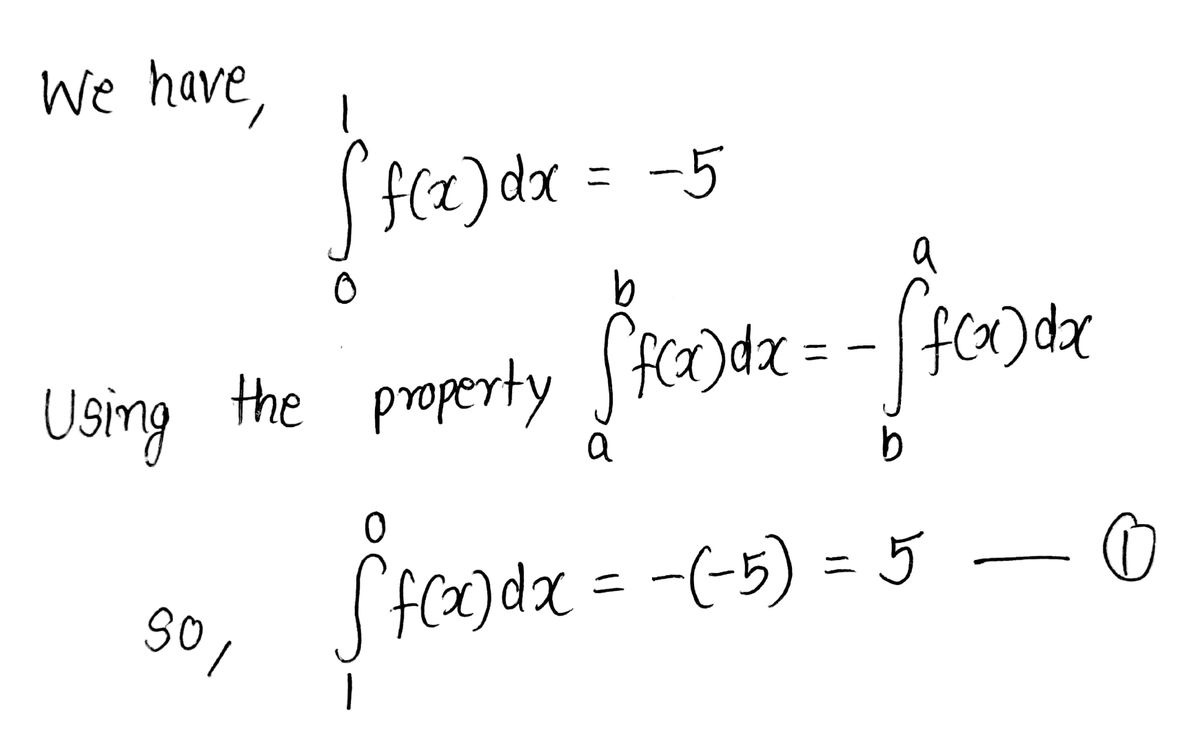
#Integral in calculus examples how to#
In this topic, we will go over the fundamentals of integrals as well as how to evaluate integrals. The fundamental calculus consists of finding both derivatives and integrals. Integration refers to the process of determining a function’s anti-derivative. These anti-derivatives are also known as function integrals. Integral calculus aids in the discovery of a function’s anti-derivatives. A function’s integral represents a family of curves. Indefinite integral and then take up definite integral.Finding integrals is the inverse process of finding derivatives. ‘b’ is called the upper limit and ‘a’ the lower limit of integration. is 9x 2 = 2y.Īs x changes from a to b the value of the integral changes from f (a) to f (b). Since it passes through the origin, c = 0 thus required eqn. So 3x 2 –2x +5 = A (x 2 + 5 ) + (Bx +C) (x–1)Įquating the coefficients of x 2, x and the constant terms from both sides we getĮxample: Find the equation of the curve where slope at (x, y) is 9x and which passes through the origin. Or 3x + 2 = A (x – 2) (x – 3) + B (x – 3) +C (x – 2) 2Ĭomparing coefficients of x2, x and the constant terms of both sides, we findįrom (ii) –5 ( 5 + 2B) + B – 4 (– 5 – 2B) = 3 Where u and v are two different functions of x

This method is known as Method of Substitution We put (2x + 3) = t ⇒ so 2 dx = dt or dx = dt / 2 To put z = f (x) and also adjust dz = f'(x) dxĮxample: ∫F h'(x ) dx, take ez = h(x) and to adjust dz = h'(x) dx It is sometime possible by a change of independent variable to transform a function into another which can be readily integrated. METHOD OF SUBSTITUTION (CHANGE OF VARIABLE) Note: In the answer for all integral sums we add +c (constant of integration) since the differentiation of constant is always zero.Įxamples: Evaluate the following integral: Integral calculus was primarily invented to determine the area bounded by the curves dividing the entire area into infinite number of infinitesimal small areas and taking the sum of all these small areas. Hence and this c is called the constant of integration Thus if we differentiate we can get back x n.Īgain if we differentiate and c being a constant, we get back the same x n Integral of xn with respect to variable x is equal to Hence, from equation (1), it follows that Integration is the inverse operation of differentiation and is denoted by the symbol . Integration is the reverse process of differentiation.


 0 kommentar(er)
0 kommentar(er)
